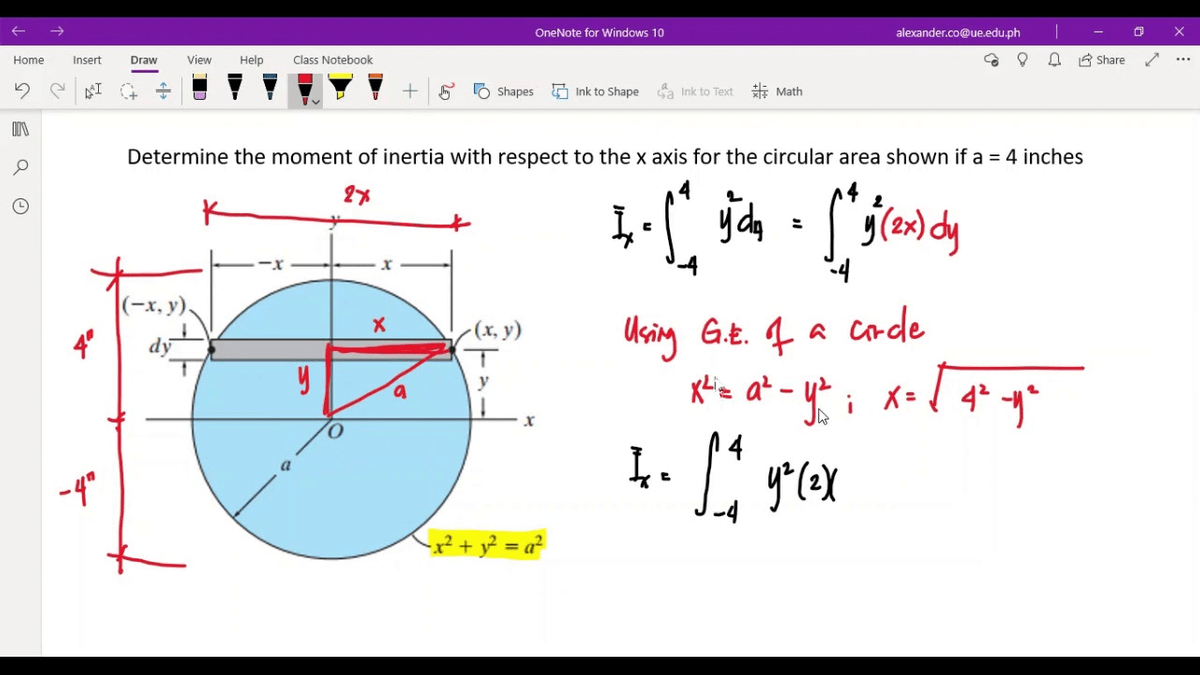
Again, we will need to describe this with an mathematical function if the height is not constant. The general form of the moment of inertia involves an integral. The moment of inertia of any extended object is built up from that basic definition. Moving from left to right, the rate of change of the area will be the height of the shape at any given \(x\)-value times the rate at which we are moving left to right. The moment of inertia of a point mass with respect to an axis is defined as the product of the mass times the distance from the axis squared.
\)) we will move left to right, using the distances from the \(y\)-axis in our moment integral (in this case the \(x\) coordinates of each point).